Capítulo 5 Los Nomencladores de clases sociales
Este capítulo tiene como propósito presentar los diversos abordajes teórico-empíricos más utilizados en el estudio de la estratificación social, a nivel internacional y nacional, fundamentalmente desde una mirada operacional.
Presentados ya los principales enfoque teóricos en el Capítulo 2, en esta sección se focaliza en las operaciones que se realizan desde el punto de vista metodológico, siguiendo criterios teóricos, para hacer posible la medición de estratos y clases sociales definidas en términos conceptuales. Para esto revisaremos algunas de las propuestas más utilizadas.
Estas preguntas guian el capítulo:
- ¿Qué enfoques teóricos sobre las clases sociales fueron operacionalizados empíricamente?
- ¿Qué diferencias presentan dichos enfoques?
- ¿Qué cuestiones aportan los enfoques nacionales?
- ¿Cómo se operacionalizan los esquemas presentados?
- ¿Cuáles son las limitaciones que presentan las fuentes de datos nacionales en la aplicación de dichos esquemas?
- ¿Sobre cuáles unidades de análisis podemos trabajar en el estudio de las clases sociales?
Al finalizar el capítulo se espera que los lectores puedan:
- Identificar las semejanzas y diferencias específicas que presenta cada nomenclador de clases propuesto por los autores aquí revisados.
- Conocer cuáles son las principales variables que sustentan a cada esquema.
- Adquirir la práctica en la operacionalización de variables complejas como la clase social.
- Establecer críticamente qué esquema utilizar según el marco teórico propuesto.
Para una mayor comprensión del capítulo recomendamos la lectura de los siguientes documentos:
Clemenceau, L., Fernández Melián, M. C., y Rodríguez de la Fuente, J. (2016). Análisis de esquemas de clasificación social basados en la ocupación desde una perspectiva teórica-metodológica comparada. Documentos de Jóvenes Investigadores IIGG, 44.
Francés García, F. J. (2009). Elementos para el estudio de la estratificación social en las sociedades avanzadas: Estrategias operativas. Revista Obets, 3.
Torrado, S. (1998b). La medición empírica de las clases sociales. En Familia y diferenciación social. Buenos Aires: Eudeba.
Sacco, N. (2019). Estructura social de la Argentina, 1976-2011. Trabajo y sociedad, (32), 25–51, (Anexo metodológico).
Carabaña, J. (1997). Esquemas y estructuras. Revista crítica de ciências sociais, (49), 67-91.
Barozet, E. (2007). La variable ocupación en los estudios de estratificación social.
Sautu, R., Dalle, P., Otero, M. P., y Rodríguez, S. (2007). La construcción de un esquema de clases a partir de datos secundarios. (Documento de Cátedra II. 4). Metodología de la Investigación Social II, Cátedra Sautu, Facultad de Ciencias Sociales-UBA.
Rodríguez de la Fuente, J. J. (2020). Del origen de clase a las condiciones de vida actuales. Movilidad social y bienestar material en la Ciudad de Buenos Aires (2004-2015). Buenos Aires: Teseo Press. (Capítulo 2. Diseño Metodológico)
5.1 De las clases en el papel a las clases en la computadora
5.1.1 Operacionalizando el concepto de clase
El proceso de operacionalización implica el pasaje de conceptos teórico-abstractos a indicadores empíricos, es decir, la transformación de un fenómeno no observable o latente, en observable (D’Ancona, 1996). Bourdieu (1990), en referencia a la conceptualización científica de las clases sociales, denominó a este proceso como la construcción de clases “en el papel”, en tanto funcionan como constructos que son agrupaciones probables fundadas en la posición que los individuos presentan en el espacio social. De este modo, las clases son construcciones analíticas pero bien fundadas en la realidad ya que proporcionan una explicación más completa del mayor número de diferencias observadas entre los agentes (Bourdieu, 1990, p. 130).
Estas clases-constructos no son clases equiparables a las que podemos percibir y comprender como existentes en la realidad social, aunque presenten probabilidades de serlo. Ejemplificando, si nuestro esquema de clasificación nos indica que un individuo asalariado y administrativo de un organismo estatal, forma parte de la “clase media”, eso no significa que esa categoría de clase tenga una relación directa con lo que en la realidad los propios individuos identifican como clase media (que de por sí presenta una gran heterogeneidad), ni con lo que las propias teorías pueden entender como “clase media” .
Las clases sociales son una parte de lo que normalmente conceptualizamos como “estructura social”. En tanto parte, el proceso de operacionalización, es decir, de separación de aspectos que suelen estar integrados (tales como la clase, el género, los vínculos sociales, la acción política, entre otros), implica una abstracción y un recorte realizado sobre la realidad, pero que permite un acercamiento a la comprensión de la misma:
Como hemos visto, los esquemas de clase son en realidad el producto de la disolución de las estructuras sociales. La fórmula para su producción podría ser algo como lo que sigue: tómense estructuras cuyos elementos son individuos, roles o acciones cualesquiera, rómpase las relaciones que haya entre sus miembros de modo que estos queden flotando libremente y sométase el magma resultante a centrifugación hasta que se haya reunido los elementos homogéneos. Una vez terminado el proceso, calcúlense los porcentajes. Se obtiene así una descripción de la estructura social (Carabaña, 1997, p. 85).
Resumiendo, si la estructura de clases es un aspecto de la estructura social, los esquemas de medición de clase son una aproximación al estudio de las mismas. Aunque se construyen a partir de la teoría, no deben entenderse como “puentes directos” entre ambos ámbitos, sino más bien como constructos estadísticos elaborados por los investigadores para aproximarse a la realidad a partir de los datos.
5.2 Enfoques operacionalizables de clases y estratos sociales
En el Capítulo 2 repasamos brevemente algunas de las teorías más importantes en el campo del estudio de las clases y la estratificación social. En este apartado nos enfocaremos en el proceso que dichos investigadores atravesaron para llevar las clases de la teoría a los papeles (o bien, a la computadora). De esta forma, nos preguntamos:
- ¿Qué decisiones han tenido que tomar?
- ¿Qué limitaciones han encontrado en el pasaje de la teoría a lo empírico?
- ¿Qué variables utilizaron para llevar a cabo dicho trabajo? ¿Cómo las combinaron?
- ¿Qué limitaciones presentan las propuestas en función de las fuentes de datos disponibles en Argentina?
Como veremos el trabajo de desentrañar las decisiones que llevaron adelante los investigadores en la elaboración de esquemas y escalas de estratificación social no siempre es una tarea sencilla, y depende en gran medida de las huellas y directrices que los propios autores han dejado en sus trabajos acerca de cómo generar dichos constructos. Algunos han elaborado anexos, trabajos o publicaciones específicas en donde han señalado cómo construir dichos instrumentos. Otros, en cambio, han sido más ambiguos en sus formulaciones metodológicas, generando que aquellos interesados en la utilización de sus enfoques elaboren esquemas aproximados.
En este sentido, proponemos un repaso de las principales decisiones, criterios y características que asumen las clasificaciones más utilizadas tanto a nivel internacional como nacional en el estudio de las clases y la estratificación social. Vale decir que esta revisión lejos está de ser exhaustiva de todos los enfoques, por esta razón, hacia el final de este apartado listaremos algunas referencias para quien desee explorar en otros formatos clasificatorios.
5.2.1 Esquemas internacionales
5.2.1.1 Esquema EGP
El esquema EGP (Erikson, Goldthorpe, & Portocarero, 1979) es uno de los más utilizados, tanto en términos internacionales como regionales, para el estudio de la estructura de clases como de la movilidad social. John Goldthorpe fue quien se encargó de popularizarlo a través de sus investigaciones, llegando a ser utilizado, a partir de una adaptación, por la European Statistical Office como clasificación oficial (European Socio-economic Classification) 4.
Según el autor, el esquema no debe considerarse como un mapa definitivo de la estructura de clases, sino como un instrumento de trabajo que puede sufrir cambios y modificaciones. En la construcción del mismo, intervinieron tanto ideas teóricas como consideraciones prácticas que dependieron del contexto en el que tuvo origen, de los propósitos y de la naturaleza de la información sobre la que sería aplicado (Erikson & Goldthorpe, 1992, p. 32).
En referencia a los criterios operacionales que implica la construcción del esquema, se consideran (Méndez & Gayo, 2007, p. 146):
1. la propiedad de los medios de producción,
2. la existencia y número de empleados (para aquellos que no son asalariados),
3. la distinción no manual – manual – agrícola, y
4. el tipo de relación de empleo (de servicios o relación contractual).
En la siguiente esquema se detallan los principales criterios de clasificación y la asignación de las clases.
Gráfico 5.1: Derivación del esquema de clases EGP. Fuente: Erikson y Goldthorpe (1992)
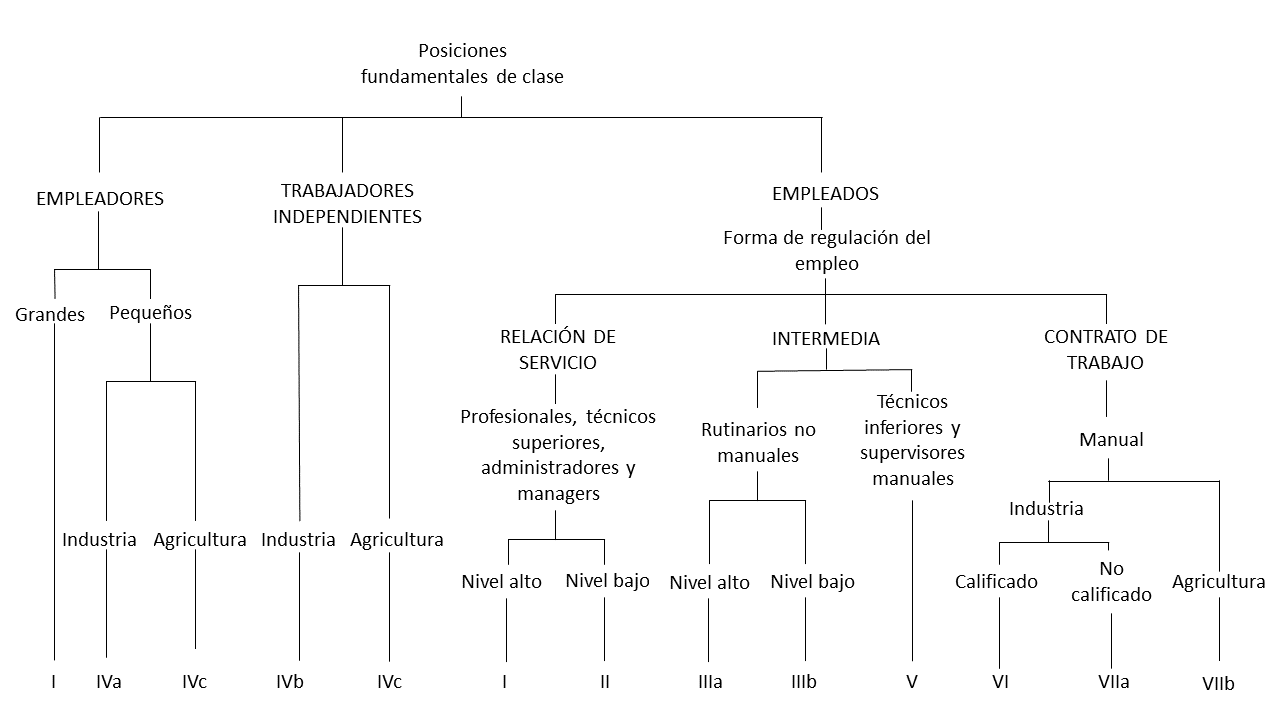
De esta forma, la primera gran división ocurre a nivel de relaciones de producción, diferenciando entre empleadores (employers), trabajadores autónomos (self-employed workers) y empleados (employees). Para el caso de los empleadores se diferencia además según si presentan empresas grandes o pequeñas, así como por su rama de actividad (industria o agricultura), al igual que en los trabajadores autónomos. La operacionalización se complica al desagregar el mundo asalariado. Aquí interviene el criterio del tipo de relaciones de empleo.
La relación de servicio da lugar a lo que el autor denomina “clase de servicios” y que esta conformada por empleados profesionales, administradores y directivos. Los contratos suelen pautarse a largo tiempo y el modo de intercambio empleador-empleado suele ser difuso, en el sentido que no sólo actúa el salario como forma de pago, sino que también ciertos elementos prospectivos (aumentos, seguros sociales, pensiones, etc.) que garantizan la estabilidad y el sostenimiento del empleo. El empleado “de servicios” obtiene autonomía y discrecionalidad, dependiendo su rendimiento del “acuerdo moral” que existe con el empleador y no de sanciones externas. En contraposición, la relación basada en el contrato de trabajo, remite a lo que en términos agregados puede entenderse como “clase obrera”. A diferencia de la relación de servicio, los contratos suelen ser de menor término y se realiza un intercambio de dinero por esfuerzo, calculado en función de las horas trabajadas. La discrecionalidad y autonomía suelen ser bajas, ya que el rendimiento del trabajador está atado a una mayor supervisión sobre el mismo y a condicionamientos externos en forma de sanciones. En medio de ambos tipos ideales de relaciones, se encuentran las formas mixtas que dan lugar a las clases intermedias.
Por otro lado, las clases (identificadas en el gráfico anterior a partir de números romanos) pueden clasificarse de distintos modos, en función de cuán desagregada se desee presentar la información —Tabla 5.1—. A nivel de mayor desagregación, el esquema cuenta con 11 clases, sin embargo los autores han trabajado con colapsamientos de 7, 5 y 3 clases.
11 clases |
7 clases |
5 clases |
|---|---|---|
I. Profesionales, administradores y oficiales de alto nivel; Directivos de grandes establecimientos industriales; Propietarios de grandes empresas |
Clase de servicio (I + II) |
Trabajadores de cuello blanco (I + II + III) |
II. Profesionales, administradores y oficiales de bajo nivel; Directivos de pequeños establecimientos industriales; Supervisores de trabajadores no manuales | ||
IIIa. Empleados de rutina no manuales de alto nivel (administración y comercio) |
Trabajadores de rutina no manuales (IIIa + IIIb) |
|
IIIb. Empleados de rutina no manual de bajo nivel (ventas y servicios) | ||
IVa. Pequeños propietarios, artesanos con empleados |
Pequeña burguesía (IVa + IVb) |
Pequeña burguesía (IVa + IVb) |
IVb. Pequeños propietarios, artesanos sin empleados | ||
IVc. Agricultores, arrendatarios y otros trabajadores cuenta propia en el sector agrícola |
Agricultores y arrendatarios (IVc) |
Trabajadores agrícolas (IVc + VIIb) |
V. Técnicos de nivel inferior, supervisores de trabajos manuales |
Trabajadores calificados (V + VI) |
Trabajadores calificados (V + VI) |
VI. Trabajadores manuales calificados | ||
VIIa. Trabajadores manuales semicalificados y no calificados |
Trabajadores no calificados (VIIa) |
Trabajadores no calificados (VIIa) |
VIIb. Trabajadores agrícolas |
Trabajadores agrícolas (VIIb) |
|
Fuente: Erikson y Goldthorpe (1992) | ||
Si bien existe bibliografía (Erikson & Goldthorpe, 1992; Rose & Harrison, 2007b) en la que se señalan algunos indicios sobre cómo operacionalizar el esquema EGP, no hay una forma directa y unívoca de realizarlo. Goldthorpe y Heath (1992) han realizado el ejercicio de operacionalización del mismo, pero para ser utilizado con la clasificación estandarizada de ocupaciones inglesa, que se diferencia tanto de la CIUO-88 como de la CIUO-08.
Comúnmente, los investigadores interesados en utilizar la clasificación han partido de una adaptación realizada por Ganzeboom para SPSS 5, a partir del clasificador ocupacional CIUO-88. Existe un paquete para R llamado ocuppar, que retoma la propuesta de Ganzeboom para ser utilizada bajo dicho programa. En el apartado siguiente, a modo de ejemplo retomaremos dicha propuesta de operacionalización.
5.2.1.2 Esquema de Wright
Como hemos señalado en el Capítulo 2, Wright ha presentado dos propuestas operacionalizables de clases, desde un enfoque neo-marxista: uno basado en las posiciones de las relaciones de clase y otro de las explotaciones múltiples. En este caso presentaremos los principales criterios abordados por el autor para el desarrollo de la segunda propuesta6.
Influenciado por el marxismo analítico, Wright identificó cuatro tipos de bienes de explotación posibles de ser relevamos empíricamente, y que se traducen en los diferentes tipos de derechos y poderes (recursos tangibles e intangibles) que tienen los sujetos en las relaciones de producción (Wright, 2005):
-
Fuerza de trabajo (explotación feudal),
- Los medios de producción (explotación capitalista),
- Los bienes de organización (explotación estatal) y
- Las cualificaciones (explotación socialista)
De este modo, la combinación de esos cuatro tipos de bienes de explotación, permiten la generación de 12 posiciones de clase (Wright, 1994).
Ahora bien, ¿Cómo llega Wright a operacionalizar dicho esquema? En este sentido, el autor es bastante franco y sincero ya que explicita todas sus decisiones y limitaciones, señalando que de este modo “los que lo deseen puedan repetir los resultados que aquí hemos presentado, y hará también que nuestras decisiones operacionales queden lo más abiertas posibles a la crítica” (Wright, 1994). Esto es de vital importancia en el campo científico, en donde la posibilidad de reproducir los resultados realizados en distintos contextos de investigación.
Es necesario aclarar que para abordar la estructura de clases desde el enfoque propuesto por Wright se torna crucial realizar un relevamiento que recabe ciertos indicadores específicos vinculados directamente con el enfoque teórico del que parte el autor 7.
Por ejemplo, tomando una de las dimensiones más complejas a ser medidas como los bienes de organización, el autor construye dos tipologías (de toma de decisiones y de autoridad) y una categoría dicotómica de posiciones jerárquicas que derivan luego en una tipología de posiciones directivas, de acuerdo con la Tabla 5.2.
Variable input |
Variable construida |
||
|---|---|---|---|
Tipología de decisión |
Tipología de decisión |
Directivo o supervisor en la jerarquía formal de la organización |
Tipología de posiciones directivas |
3 |
3 o 4 |
Sí |
1. Directivo según todos los criterios |
3 |
3 o 4 |
No |
2. Directivo fuera de la jerarquía formal |
3 |
1 o 2 |
Sí |
3. Directivo no supervisor |
3 |
1 o 2 |
No |
4. Decisor no supervisor fuera de jerarquía formal |
2 |
3 o 4 |
Sí |
5. Directivo-asesor según todos los critarios |
2 |
3 o 4 |
No |
6. Asesor fuera de la jerarquía formal |
2 |
1 o 2 |
Sí |
7. Asesor no supervisor |
2 |
1 o 2 |
No |
8. Asesor no supervisor fuera de la jerarquía formal |
1 |
4 |
Sí |
9. Supervisor sancionador |
1 |
3 |
Sí |
10. Supervisor de tareas |
1 |
2 |
Sí |
11. Supervisor nominal en la jerarquía |
1 |
4 |
No |
12. Supervisor sancionador fuera de la jerarquía formal |
1 |
3 |
No |
13. Supervisor de tareas fuera de la jerarquía |
1 |
1 |
Sí |
14. Sin subordinados pero en la jerarquía |
1 |
1 o 2 |
No |
15. No supervisor / no directivo según todos los criterios |
Fuente: Wright (1994) | |||
Finalmente la tipología de bienes de organización, permite discriminar a las personas en función de si son directivos, supervisores o no-directivos. Como pudimos ver, para llegar a esa tipología, distintas operaciones complejas debieron realizarse desde los indicadores relevados hasta la construcción de tipologías intermedias.
5.2.1.3 Propuestas gradacionales
Los enfoques de tipo gradacional son tributarios del paradigma estructural-funcionalista que ha orientado a las ciencias sociales durante gran parte de la mitad del siglo XX. Dichas propuestas sostienen básicamente que partiendo de las características atributivas (ingresos, estatus, prestigio), los individuos son posicionados en un continuum en el que las fronteras de clase se tornan difusas. A diferencia de los enfoques (neo)marxistas o (neo)weberianos, estas propuestas de medición ponen el eje en el carácter jerárquico de las ocupaciones, principalmente en función de la importancia de las mismas en relación al conjunto del sistema social, el prestigio y las recompensas materiales que se derivan de las posiciones ocupadas (Ossowski, 2003; Parsons, 1954; Wright, 1979).
En términos operacionales, estas gradaciones pueden constituirse de forma simple o sintética en función de cuantas variables intervengan en su determinación. Asimismo, los aspectos a medir pueden tener una naturaleza objetiva o subjetiva (Cachón Rodríguez, 1989). Sin embargo, su utilización en estudios internacionales, no sólo se explica por su fundamentación teórica, sino también por las ventajas metodológicas que su utilización implica. Por un lado, son escalas de medición con un gran nivel de estandarización, por lo que pueden ser utilizadas a partir de la información socio-ocupacional relevada en todos los países. Por el otro, su carácter continuo garantiza la aplicabilidad de diversas técnicas frecuentemente utilizadas como regresiones lineales, path analysis o análisis factoriales.
De esta forma, si bien existe un número importante de enfoques gradacionales de ocupación, señalaremos brevemente dos de los más relevantes: la Standard International Occupational Prestige Scale (SIOPS) de Treiman y el Internacional Socio-Economic Index (ISEI) de Treiman, Ganzeboom y de Graaf (Bergman & Joye, 2001; Francés García, 2009). Ambos toman a la ocupación como el indicador principal del posicionamiento en la jerarquía social, pero mientras uno mide el prestigio de las ocupaciones, el otro cuantifica el estatus socioeconómico de las mismas.
El primero de estos (SIOPS), hace referencia a las clásicas escalas de prestigio ocupacional que, basadas en indicadores subjetivos, relevaron el grado de aprobación y respeto que presentaba un set de ocupaciones para las distintas personas. Según Treiman, los puntajes de prestigio obtenidos eran similares entre distintos sectores poblacionales (ricos o pobres, jóvenes o viejos) y entre distintos países del mundo. El prestigo, de este modo, era un proxy válido de la importancia funcional que las ocupaciones presentaban en la sociedad. En términos operativos, dicha escala recopila las puntuaciones medias de prestigio de aproximadamente 60 países, utilizando como base la CIUO-68. A continuación —Tabla 5.3— presentamos, a modo de ejemplo, las puntuaciones de 20 ocupaciones seleccionadas, entre las 509 rankeadas en total (Treiman, 1977).
Ocupación |
Puntaje estandard |
|---|---|
Jefe de Estado |
90 |
Oficial de policía de alto grado |
75 |
Científico social |
69 |
Ingeniero eléctrico |
65 |
Osteópata |
62 |
Empresario |
58 |
Corredor de bolsa |
56 |
Experto en huellas dactilares |
54 |
Agente de ventas |
51 |
Agente inmobiliario |
49 |
Operador de garage |
47 |
Fotógrafo |
45 |
Ingeniero en locomotoras |
43 |
Grabador de metales |
41 |
Contratista agrícola |
39 |
Músico de Jazz |
38 |
Comerciante |
36 |
Herrero |
34 |
Cartero |
33 |
Cajero |
31 |
Sacristán |
30 |
Reparador de bicicletas |
28 |
Deshollinador |
25 |
Sereno |
22 |
Transportista de animales |
18 |
Recolector de residuos |
13 |
Fuente: Treiman (1997) | |
Como puede observarse dentro de las ocupaciones más prestigiosas se encuentran la de “jefe de estado” y “alto oficial de policía”, mientras que las de menos puntaje están el “recolector de basura” y el “transportista de animales”.
La otra familia de escalas continuas de ocupación pueden representarse a partir del ISEI. En tanto índice socioeconómico, es construido a partir de información objetiva, específicamente de la suma ponderada de información de ingresos y del nivel educativo. Una primera versión de los índices elaborados con este método es el Socio-Economic Index (SEI) elaborado por Duncan en 1961 sobre la estructura ocupacional de Estados Unidos (Blau & Duncan, 1967; Duncan & Hodge, 1963). En particular, el SEI se construía a partir de un análisis de regresión en el que se consideraba el prestigio ocupacional de 45 ocupaciones de 1949 como variable dependiente y los ingresos medios y el nivel educativo como variables independientes, controlando por la edad. De este modo, con los resultados de la ecuación se podían estimar los puntajes de estatus de todo el rango de ocupaciones de la fuerza de trabajo. Para su construcción, Duncan utilizó los títulos de prestigio ocupacional presentes en el estudio sobre prestigio (NORC) de 1947 de North-Hatt y el censo de Estados Unidos de 1950. En la Tabla 5.4 se resumen algunas de las ocupaciones que conforman el SEI y su puntaje estimado.
Intervalo de puntaje |
Ocupaciones de ejemplo |
|---|---|
90-96 |
Arquitectos, dentistas, ingenieros químicos |
85-89 |
Ingenieros aeronáuticos,ingenieros industriales, gerentes de bancos |
80-84 |
Profesores universitarios, editores y reporteros, ingenieros eléctricos |
75-79 |
Contadores y auditores, químicos, veterinarios |
70-74 |
Diseñadores, maestros, jefes de departamento |
65-69 |
Artistas y maestros de arte, dibujantes, gerentes de ventas de vehículos |
60-64 |
Bibliotecarios, instructores de deportes, administradores de correo |
55-59 |
Directores de funerarias y embalsamadores, conductor ferroviario, propietario de tiendas |
50-54 |
Clérigos, músicos y maestros de música, oficiales y admistradores públicos |
45-49 |
Topógrafos, gerentes de talleres de automóviles, operadores de maquinarias de oficina |
40-44 |
Propietario de transporte, cajeros, electricistas |
35-39 |
Vendedores de comercio, encuadernadores, reparadores de TV y radio |
30-34 |
Administradores de edificios, propietarios de gasolinerías, caldereros |
25-29 |
Mensajeros, albañiles, yeseros |
20-24 |
Mensajeros telegráficos, panaderos, choferes de autobuses |
15-19 |
Herreros, carpinteros, pintores |
10-14 |
Agricultores, zapateros, tintoreros |
5-9 |
Vendedores ambulantes, conserjes, trabajadores de la construcción |
0-4 |
Trabajadores de minas, porteros, trabajadores de molino |
Fuente: elaboración propia en base a Blau y Duncan (1967) | |
Posteriormente, Ganzeboom, Treiman y de Graaf (1992) modificaron la ecuación de cálculo del SEI, considerando los efectos directos e indirectos de la educación, la edad y la ocupación sobre los ingresos, para elaborar el nuevo índice internacional. Asimismo, la construcción del ISEI implicó el uso 31 fuentes de información de 16 países entre 1968 y 1982. A diferencia de Duncan, estos autores no tuvieron en cuenta al prestigio de las ocupaciones durante la construcción del índice, que fue actualizado en dos ocasiones posteriormente. En la Tabla 5.5, se muestran los puntajes obtenidos a mayor y menor nivel de agregación para las primeras ocupaciones de la CIUO-68.
Nombre de las ocupaciones |
Gran grupo |
Grupo menor |
Grupo unitario |
|
|---|---|---|---|---|
0/1000 |
Profesionales, técnicos y trabajadores relacionados |
67 |
||
0100 |
CIENTÍFICOS DE LA FÍSICA Y TÉCNICOS RELACIONADOS |
62 |
||
0100 |
Químicos |
73 |
||
0120 |
Físicos |
79 |
||
0130 |
Otros científicos físicos |
79 |
||
0140 |
Técnicos en ciencias de la física |
47 |
||
0200 |
ARQUITECTOS E INGENIEROS |
71 |
||
0210 |
Arquitectos |
77 |
||
0220 |
Ingenieros civiles |
73 |
||
0230 |
Ingenieros eléctricos y electrónicos |
69 |
||
0240 |
Ingenieros mecánicos |
68 |
||
0250 |
Ingenieros químicos |
73 |
||
0260 |
Metalúrgicos |
70 |
||
0270 |
Ingenieros en minas |
65 |
||
0280 |
Ingenieros industriales |
65 |
||
0290 |
Otros ingenieros |
76 |
||
0300 |
TÉCNICOS - INGENIEROS |
53 |
||
0310 |
Topógrafos |
58 |
||
0320 |
Dibujantes |
53 |
||
0330 |
Técnicos en ingeniería civil |
50 |
||
0340 |
Técnicos en ingeniería electrónica y eléctrica |
48 |
||
Fuente: elaboración propia en base a Ganzeboom, Treiman y de Graaf (1992) | ||||
Al igual que en el caso del esquema EGP, en la página de Harry Ganzeboom 8 puede encontrarse información y las sintaxis para SPSS de clasificación del ISEI y SIOPS partiendo de la CIUO-88. El paquete ocuppar para R también permite su construcción automática.
5.2.2 Esquemas nacionales
5.2.2.1 Propuesta de Germani
Gino Germani, además de ser reconocido como uno de los fundadores de la sociología académica argentina, fue uno de los pioneros en el estudio de las clases sociales a partir de información censal y de encuestas de hogares. Tal como señala Murmis (Germani, Germani, Mera, & Rebón, 2010) su enfoque ecléctico, estuvo influenciado tanto por la escuela marxista como por la funcionalista y por los estudios norteamericanos de estratificación social vinculados al análisis estadístico.
Centrándonos en sus libros y artículos más importantes (Germani, 1955, 1963, 2010) si bien su aproximación empírica a la cuestión se baso en el uso de esquemas de clases sociales, también ha utilizado escalas de nivel socio-económico (relevando diversos aspectos objetivos de la posición de los individuos) y escalas de prestigio. Sin embargo, aquí haremos un breve repaso de su propuesta de operacionalización de las clases sociales.
Para el autor, las clases sociales presentaban tres características centrales:
Eran formas de agrupación que tenían un rol central en el funcionamiento y organización de las sociedades;
no eran meras nominaciones científicas, sino que tenían una existencia sociológica real;
No podían explicarse únicamente a través de la información ocupacional, sino que deberían considerarse aspectos psicosociales y ligados al “tipo de existencia” de los individuos, aunque existan limitaciones en los datos para abordar dicha dimensión.
Asimismo, Germani señaló que su propuesta de operacionalización podía ser modificada y adaptada en el tiempo ya que era en vano buscar una discriminación neta de dichos agrupamientos debido a la complejidad de combinaciones entre criterios estructurales y psicosociales. Las clases, entonces, se definían a partir de un criterio espacial y probabilístico, es decir, como “zonas de la estructura social en la que cierta combinación de criterios se da con mayor frecuencia estadística” (Germani, 1955, p. 143).
Respecto al esquema de clasificación propuesto por el autor, el mismo recurre a “la convencional clasificación tripartita” de clase alta, media y popular (1955, p. 146). La clase alta, debido a su bajo peso poblacional, es incluida dentro de las clases medias. Asimismo, tanto las clases populares como las clases medias son desagregadas según sector de actividad (sector urbano y sector rural) y de acuerdo a su estatus ocupacional (trabajadores dependientes e independientes) (1955, pp. 146–147). La frontera entre ambas clases se basaba en la distinción manual / no manual del trabajo, existiendo una amplia heterogeneidad dentro de cada agregado —Tabla 5.6—.
Categorías de ocupación |
Clases sociales |
|---|---|
Obreros y aprendices |
Clases Populares |
Trabajadores a domicilio y cuenta propia | |
DEPENDIENTES |
Clases medias (y alta) |
Empleados, cadetes | |
Jubilados, pensionados | |
AUTÓNOMOS | |
Propietarios agropecuarios | |
Propietarios industriales | |
Propietarios comercio y servicios | |
Profesionales liberales | |
Rentistas | |
Fuente: elaboración propia en base a Germani (1955) | |
5.2.2.2 Propuesta de Torrado
En tanto continuadora de la tradición inaugurada por Germani, Torrado aportó un formato de medición específico para el análisis de la estructura de clases argentina. La propuesta de la autora tiene, al menos dos versiones operacionalizables: una primigenia, producto de su trabajo en colaboración con de Ipola (Ipola & Torrado, 1976) y una versión posterior, más acabada, que constituyó la base de su obra “Estructura social de la Argentina” (Torrado, 1992) y que fue resultado de diversas intentos de clasificación (CFI, 1988; Torrado & Rofman, 1988b).
En palabras de la autora, su propuesta de esquema de clases mantenía un compromiso con tres de los principales enfoques de estratificación existentes: el “funcionalista”, que tiende a ofrecer una visión jerárquica de la estructura; el “materialista”, que define a las clases en función a las relaciones de producción y el “estadístico” o “pragmático” que hace hincapié en la utilización de categorías homogéneas que permitan comparabilidad de la información estadística (Torrado, 1998b).
Torrado acude a cinco variables que conformarán lo que podríamos denominar como el “esqueleto” de las clases sociales:
- la ocupación;
- la categoría ocupacional;
- el sector de actividad;
- el tamaño del establecimiento y
- la rama de actividad.
Particularmente la ocupación, captada a partir de la CIUO-68, es re-clasificada para conformar nueve grupos de ocupación (GO) —Tabla 5.7—: 1) Empresarios, directores de empresas y funcionarios públicos superiores; 2) Propietarios de establecimientos; 3) Profesionales en función específica; 4) Técnicos, docentes y supervisores; 5) Empleados y vendedores; 6) Trabajadores especializados; 7) Trabajadores no especializados; 8) Empleados domésticos y 9) Sin especificar.
Grupo de ocupación |
Empleadores |
Asalariados |
Servicio doméstico |
Cuenta propia y familiar sin remuneración |
|||
Sector privado |
Sector privado |
Sector privado |
Sector privado |
Sector público |
|||
Más de 5 ocupados |
Hasta 5 ocupados |
Más de 5 ocupados |
Hasta 5 ocupados |
||||
1. Empresarios, directores de empresas y funcionarios públicos superiores |
1.1 |
5.1 |
1.2 |
4.1.2 |
4.2 |
11 |
5.2 |
2. Propietarios de establecimientos |
3 |
4.1.1 |
|||||
3. Profesionales en función específica |
2.1.1 |
2.1.2 |
2.3.1 |
2.3.2 |
2.4 |
2.2 |
|
4. Técnicos, docentes y supervisores |
3 |
5.1 |
4.1.1 |
4.1.2 |
4.2 |
5.2 |
|
5. Empleados y vendedores |
6.1.1 |
6.1.2 |
6.2 |
||||
6. Trabajadores especializados |
8.1.1 |
8.1.2 |
8.2 |
7 |
|||
7. Trabajadores no especializados |
10 |
10 |
9.1.1 |
9.1.2 |
9.2 |
10 |
|
8. Empleados domésticos |
11 |
11 |
11 |
11 |
11 |
11 |
|
9. Sin especificar |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
Fuente: elaboración propia en base a Torrado (1998) | |||||||
De este modo, del entrecruzamiento de las distintas variables se genera una estratificación socio-ocupacional que presentamos a continuación —Tabla 5.8—, y que da lugar al clasificador de la Condición Socio-Ocupacional (CSO) en su versión desagregada.
Nº identificador |
Estrato socio-ocupacional |
Siglas |
|---|---|---|
1 |
DIRECTORES DE EMPRESAS |
DIREC |
1.1 |
Empleadores del sector privado en establecimientos con más de cinco ocupados |
DIREC (ER - SPR. TE>5) |
1.2 |
Asalariados del sector privado en establecimientos con más de cinco ocupados |
DIREC (AS - SPR. TE>5) |
2 |
PROFESIONALES EN FUNCIÓN ESPECÍFICA |
PROF |
2.1 |
Empleadores del sector privado |
PROF (ER – SPR) |
2.1.1 |
En establecimientos con más de cinco ocupados |
PROF (ER- SPR. >5) |
2.1.2 |
En establecimientos con hasta cinco ocupados |
PROF (ER- SPR. <=5) |
2.2 |
Cuenta propia |
PROF (CP) |
2.3 |
Asalariados del sector privado |
PROF (AS-SPR) |
2.3.1 |
En establecimientos con más de cinco ocupados |
PROF (AS- SPR. >5) |
2.3.2 |
En establecimientos con hasta cinco ocupados |
PROF (AS- SPR. <=5) |
2.4 |
Asalariados del sector público |
PROF (AS- SPU) |
3 |
PROPIETARIOS DE PEQUEÑAS EMPRESAS |
PPE |
4 |
CUADROS TÉCNICOS Y ASIMILADOS |
TECN |
4.1 |
Asalariados del sector privado |
TECN (AS-SPR) |
4.1.1 |
En establecimientos con más de cinco ocupados |
TECN (AS -SPR. TE>5) |
4.1.2 |
En establecimientos con hasta cinco ocupados |
TECN (AS -SPR. TE<=5) |
4.2 |
Asalariados del sector público |
TECN (AS -SPU) |
5 |
PEQUEÑOS PRODUCTORES AUTÓNOMOS |
PPA |
5.1 |
Empleadores del sector privado en establecimientos con hasta cinco ocupados |
PPA (ER - SPR. TE <=5) |
5.2 |
Cuenta propia |
PPA (CP) |
6 |
EMPLEADOS ADMINISTRATIVOS Y VENDEDORES |
EAV |
6.1 |
Asalariados del sector privado |
EAV (AS-SPR) |
6.1.1 |
En establecimientos con más de cinco ocupados |
EAV (AS - SPR. TE>5) |
6.1.2 |
En establecimientos con hasta cinco ocupados |
EAV (AS - SPR. TE<=5) |
6.2 |
Asalariados del sector público |
EAV (AS - SPU) |
7 |
TRABAJADORES ESPECIALIZADOS AUTÓNOMOS |
TEA |
8 |
OBREROS CALIFICADOS |
OCAL |
8.1 |
Asalariados del sector privado |
OCAL (AS – SPR) |
8.1.1 |
En establecimientos con más de cinco ocupados |
OCAL (AS - SPR. TE>5) |
8.1.2 |
En establecimientos con hasta cinco ocupados |
OCAL (AS - SPR. TE<=5) |
8.2 |
Asalariados del sector público |
OCAL (AS - SPU) |
9 |
OBREROS NO CALIFICADOS |
ONCAL |
9.1 |
Asalariados del sector privado |
ONCAL (AS – SPR) |
9.1.1 |
En establecimientos con más de cinco ocupados |
ONCAL (AS - SPR. TE>5) |
9.1.2 |
En establecimientos con hasta cinco ocupados |
ONCAL (AS - SPR. TE<=5) |
9.2 |
Asalariados del sector público |
ONCAL (AS - SPU) |
10 |
PEONES AUTÓNOMOS |
TMARG |
11 |
EMPLEADOS DOMÉSTICOS |
EDOM |
12 |
SIN ESPECIFICAR CSO |
SESP |
Fuente: Torrado (1998) | ||
En su versión agregada el nomenclador discrimina once estratos socio-ocupacionales, mientras que en su versión desagregada, dichos estratos son subdivididos en función del sector de actividad y la categoría ocupacional. Mientras que la ocupación, la categoría ocupacional y el tamaño del establecimiento, permiten establecer diferenciaciones verticales en la estratificación (formando, según la autora, capas sociales), la rama y el sector de actividad, permite diferenciar a los estratos en términos horizontales, es decir, en fracciones de clase. Finalmente, el nomenclador puede ser agregado en tres clases sociales —Tabla 5.9—, definidas por la autora como clase alta, media y obrera, terminologías que “se relacionan más con la forma simbólica en que dichos colectivos existen en la cultura política argentina, que con una adhesión más explícita a algunas de las incontables teorizaciones existentes (…)” (Torrado, 1998b, p. 236).
Clase social |
Estratos sociales |
Estratos sociales |
|---|---|---|
Clase alta |
- |
Directores de empresa |
Clase media |
Autónomos |
Profesionales en función específica |
Propietarios de pequeñas empresas | ||
Pequeños productores autónomos | ||
Asalariados |
Profesionales en función específica |
|
Cuadros técnicos y asimilados | ||
Empleados administrativos y vendedores | ||
Clase obrera |
Autónomos |
Trabajadores especializados autónomos |
Asalariados |
Obreros calificados |
|
Obreros no calificados | ||
Marginales |
Peones autónomos |
|
Empleados domésticos | ||
Fuente: elaboración propia en base a Torrado (1998) | ||
5.3 Operacionalización paso a paso
Paquetes que utilizaremos en este subcapítulo:
En este apartado practicaremos el método de operacionalización tradicional. Usando como referencia el texto de “La medición empírica de las clases sociales” (Torrado, 1998b), seguiremos los pasos de la autora para llegar en primer lugar a un nomenclador de la Condición Socio-Ocupacional (CSO) y posteriormente a un sistema de clases sociales de 3 clases que puede ser subdividido en estratos.
Como hemos dicho la transformación de un concepto complejo como el de “clase social” a un esquema empírico que permita su medición, implica una serie de pasos en los que es necesario prestar atención y ser sumamente ordenado. Los pasos a seguir serán los siguientes:
1. Presentaremos la propuesta de la autora, en la que señala como a partir de distintas combinaciones entre categorías de las variables consideradas surgen posiciones socio-ocupacionales.
Transformaremos y crearemos algunas variables de la EPH necesarias para la construcción del esquema.
Presentaremos el código para la construcción del nomenclador CSO.
Crearemos el sistema clasificatorio de clases sociales y lo probaremos.
5.3.1 Punto de partida
Como hemos señalado la autora parte de 5 variables para la construcción de su esquema de clases: la ocupación (agrupada en grupos ocupacionales), la categoría ocupacional, el sector de actividad, el tamaño del establecimiento y la rama de actividad (que no utilizaremos en este caso). A continuación presentamos la Tabla 5.10 de doble entrada que da lugar a las posiciones del nomenclador (Torrado, 1998b, p. 232), que ya hemos revisado en el apartado anterior:
Grupo de ocupación |
Empleadores |
Asalariados |
Servicio doméstico |
Cuenta propia y familiar sin remuneración |
|||
Sector privado |
Sector privado |
Sector privado |
Sector privado |
Sector público |
|||
Más de 5 ocupados |
Hasta 5 ocupados |
Más de 5 ocupados |
Hasta 5 ocupados |
||||
1. Empresarios, directores de empresas y funcionarios públicos superiores |
1.1 |
5.1 |
1.2 |
4.1.2 |
1.1* |
11 |
5.2 |
2. Propietarios de establecimientos |
3 |
4.1.1 |
4.2 |
||||
3. Profesionales en función específica |
2.1.1 |
2.1.2 |
2.3.1 |
2.3.2 |
2.4 |
2.2 |
|
4. Técnicos, docentes y supervisores |
3 |
5.1 |
4.1.1 |
4.1.2 |
4.2 |
5.2 |
|
5. Empleados y vendedores |
6.1.1 |
6.1.2 |
6.2 |
||||
6. Trabajadores especializados |
8.1.1 |
8.1.2 |
8.2 |
7 |
|||
7. Trabajadores no especializados |
10 |
10 |
9.1.1 |
9.1.2 |
9.2 |
10 |
|
8. Empleados domésticos |
11 |
11 |
11 |
11 |
11 |
11 |
|
9. Sin especificar |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
* Modificación respecto a la propuesta de Torrado | |||||||
La tarea fundamental es ir elaborando un código que permita “ubicar” a las personas de la base de datos en cada una de las celdas. Dicha tabla es una buena ayuda-memoria para saber que casos fueron ya clasificados a medida que vamos armando el código, y conocer que situaciones nos faltaría clasificar. Como toda variable, el CSO debe ser exhaustivo (contemplar todas las posiciones posibles) y excluyente (un caso no puede tomar dos posiciones distintas).
5.3.2 Acondicionando la base
En este caso, seguiremos utilizando la base de la EPH del segundo trimestre de 2015.
En primer lugar vamos a descomponer los dígitos del CNO, ya que la variable PP04D_COD será la que nos proporcionará la información ocupacional. La descomposición la realizaremos fundamentalmente para trabajar separadamente con el carácter ocupacional y la calificación de la tarea. Para ello utilizaremos la función str_sub del paquete ´stringr´ (se encuentra en el tidyverse), que nos permite “partir” variables de cadena según lo solicitemos. Por último convertimos dichas variables a tipo numérica, ya que realizaremos operaciones lógicas que así lo requieren.
eph_ind_215$cno12 <- str_sub(eph_ind_215$PP04D_COD, 1, 2) #señala que parta de la posición 1 hasta 2 del código
eph_ind_215$cno3 <- str_sub(eph_ind_215$PP04D_COD, 3, 3) #señala que parta de la posición 3 a la 3 del código
eph_ind_215$cno4 <- str_sub(eph_ind_215$PP04D_COD, 4, 4)
eph_ind_215$cno5 <- str_sub(eph_ind_215$PP04D_COD, 5, 5)
eph_ind_215$cno12 <- as.numeric(eph_ind_215$cno12)
eph_ind_215$cno3 <- as.numeric(eph_ind_215$cno3)
eph_ind_215$cno4 <- as.numeric(eph_ind_215$cno4)
eph_ind_215$cno5 <- as.numeric(eph_ind_215$cno5)El segundo paso será crear una variable que permita agrupar a las ocupaciones del mismo modo que lo hizo Torrado (primera columna del gráfico anterior). Para esto generaremos la variable grupo de ocupación (GO), que, en nuestro caso, no es más que una agrupamiento entre el carácter ocupacional (dos primeros dígitos del CNO) y la calificación de la tarea (quinto dígito del CNO).
A través de la función case_when del paquete dplyr podremos asignarle un valor a la variable go en la medida que se cumplan determinadas condiciones. Para quienes trabajan con SPSS, dicha función es similar al IF. Por otro lado, a través de la función mutate crearemos la nueva variable go.
eph_ind_215$go <- NA
eph_ind_215 <- eph_ind_215 %>%
mutate(go = case_when((cno12 >= 0 & cno12 <=4) | (cno12 == 7) ~ 1,
(cno12 >= 5 & cno12 <=6) ~ 2,
(cno5 == 1) & ((cno12 >= 10 & cno12 <= 20) |
(cno12 == 32) | (cno12 >= 34 & cno12 <= 40) |
(cno12 >= 42 & cno12 <= 47) | (cno12 >= 49 & cno12 <= 54) |
(cno12 >= 60 & cno12 <= 64) | (cno12 >= 70 & cno12 <= 92)) ~ 3,
(cno5 > 4) & (cno12 == 11 | cno12 == 42 | cno12 == 43 |
cno12 == 50 | cno12 == 70 | cno12 == 81 | cno12 == 91) ~ 3,
(cno5 == 2) & ((cno12 >= 10 & cno12 <= 32) | (cno12 >= 34 & cno12 <= 54) |
(cno12 >= 56 & cno12 <= 92)) ~ 4,
(cno5 == 1) & ((cno12 == 30 | cno12 == 31 | cno12 == 41 | cno12 == 48) |
(cno12 >= 56 & cno12 <= 58) | (cno12 == 65)) ~ 4,
(cno5 == 3) & (cno12 == 40 | cno12 == 42 | cno12 == 43 | cno12 == 45 |
cno12 == 91) ~ 4,
(cno5 == 4) & (cno12 == 42 | cno12 == 43 | cno12 == 45) ~ 4,
(cno5 > 4) & (cno12 == 40 | cno12 == 41 | cno12 == 44 | cno12 == 45 |
cno12 == 46 | cno12 == 51 | cno12 == 92) ~ 4,
(cno5 == 3) & ((cno12 >= 10 & cno12 <= 32) | (cno12 == 35) | (cno12 == 41) |
(cno12 == 54) | (cno12 == 81)) ~ 5,
(cno5 == 4) & ((cno12 >= 10 & cno12 <= 11) | (cno12 >= 30 & cno12 <= 32) |
(cno12 == 35)) ~ 5,
(cno5 > 4) & ((cno12 == 10) | (cno12 >= 20 & cno12 <= 32) | (cno12 == 35)) ~ 5,
(cno5 == 1 | cno5 == 2) & (cno12 == 55) ~ 6,
(cno5 == 3) & ((cno12 == 34) | (cno12 == 36) | (cno12 == 44) |
(cno12 >= 46 & cno12 <= 53) | (cno12 >= 55 & cno12 <= 80) |
(cno12 == 82) | (cno12 == 90) | (cno12 == 92)) ~ 6,
(cno5 == 4) & ((cno12 == 44) | (cno12 == 49) | (cno12 == 53) | (cno12 == 57)) ~ 6,
(cno5 > 4) & ((cno12 == 34) | (cno12 >= 47 & cno12 <= 49) | (cno12 >= 52 & cno12 <= 54) | (cno12 >= 57 & cno12 <= 65) | (cno12 >= 71 & cno12 <= 80) | (cno12 >= 82 & cno12 <= 90)) ~ 6,
(cno12 == 33) ~ 7,
(cno5 == 4 | cno5 == 9) & ((cno12 == 20) | (cno12 == 34) |
(cno12 >= 36 & cno12 <= 41) | (cno12 >= 46 & cno12 <= 48) |
(cno12 >= 50 & cno12 <= 52) | (cno12 == 54) | (cno12 == 56) |
(cno12 >= 58 & cno12 <= 92)) ~ 7,
(cno5 >= 4) & (cno12 == 55) ~ 8
,(cno12 == 99) | (is.na(cno12)) ~ 9))Para poder hacer un primer chequeo de la variable que creamos crearemos la misma en formato factor y la etiquetaremos. Esto lo hacemos solo en términos ilustrativos, ya que no usaremos la varible posteriormente. Los casos “sin especificar” corresponden fundamentalmente a personas inactivas y desocupadas.
eph_ind_215$go_f <- factor(eph_ind_215$go, labels = c("Empresarios, directores de empresas y funcionarios públicos superiores",
"Propietarios de establecimientos", "Profesionales en función específica",
"Técnicos, docentes y supervisores", "Empleados y vendedores", "Trabajadores especializados",
"Trabajadores no especializados", "Empleados domesticos", "Sin especificar"))
table(eph_ind_215$go_f)
Empresarios, directores de empresas y funcionarios públicos superiores
140
Propietarios de establecimientos
1023
Profesionales en función específica
1326
Técnicos, docentes y supervisores
3825
Empleados y vendedores
6165
Trabajadores especializados
8399
Trabajadores no especializados
2113
Empleados domesticos
1354
Sin especificar
35683 En tercer lugar, necesitaremos recodificar dos variables más: el sector de actividad y el tamaño del establecimiento. En el primer caso, juntaremos la categoría “de otro tipo” al sector privado. De esta forma el valor 1 sera asumido por el “sector privado” y el 2 por el “sector público”. Para ello utilizamos la función recode del paquete car, que es similar a la función recode en SPSS. Para el caso del tamaño del establecimiento separaremos a los casos que trabajan en establecimientos de menos de 5 trabajadores inclusive y aquellos de más de 5. Para ello nos basaremos tanto en la variable PP04C, que mide directamente el tamaño, y la variable PP04C99, que lo mide cuando la anterior variable no es respondida (revisar el diseño de registro de la EPH para mayor comprensión de como se preguntan dichos indicadores). El valor 1 representa las empresas de menos de 5 trabajadores inclusive y el valor 2 las de más de 5 trabajadores.
eph_ind_215 <- eph_ind_215 %>%
mutate(sector_act = car::recode(eph_ind_215$PP04A, "1=2; 2:3=1"))
eph_ind_215 <- eph_ind_215 %>%
mutate(tamano = case_when((PP04C > 0 & PP04C <= 5) | (PP04C == 99 & PP04C99 ==
1) ~ 1, (PP04C > 5 & PP04C < 99) | (PP04C == 99 & PP04C99 >= 2) ~ 2, PP04C ==
0 | PP04C99 == 0 ~ NA_real_))5.3.3 Creación CSO desagregado
Con las variables necesarias ya creadas y/o recodificadas, podemos empezar a “llenar los casilleros” del cuadro anteriormente presentado. Lo que haremos es asignar a cada celda una posición en el CSO desagregado, en función de la combinación entre categorías de las variables.
A modo de ejemplo vamos mostrar como llenaríamos los casilleros de la primera fila, columna primera y segunda, es decir, directores y gerentes de empresas que son empleadores de empresas privadas de grandes establecimientos, por un lado, y de pequeños establecimientos, por el otro. En el primer caso, tres condiciones deben cumplirse, que el GO sea 1, que la categoría ocupacional sea “empleador” (valor 1) y que el tamaño del establecimiento sea mayor a 5 (valor 2). En el segundo caso, los criterios para el GO y la categoría ocupacional serán similares salvo que el tamaño del establecimiento será de menos de 5 ocupados (valor 1).
A continuación, mostramos el código completo para la construcción del CSO desagregado.
eph_ind_215 <- eph_ind_215 %>%
mutate(cso_desag = case_when(go==1 & CAT_OCUP==1 & tamano==2 ~ 1,
go==1 & CAT_OCUP==1 & tamano==1 ~ 13,
go==1 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 2,
go==1 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 2,
go==1 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 11,
go==1 & CAT_OCUP==3 & sector_act==2 ~ 1,
go==1 & CAT_OCUP==2 ~ 14,
go==1 & CAT_OCUP==4 ~ 14,
go==1 & CAT_OCUP==NA ~ 14,
go==2 & CAT_OCUP==1 & tamano==2 ~ 9,
go==2 & CAT_OCUP==1 & tamano==1 ~ 13,
go==2 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 10,
go==2 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 10,
go==2 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 11,
go==2 & CAT_OCUP==3 & sector_act==2 ~ 12,
go==2 & CAT_OCUP==2 ~ 14,
go==2 & CAT_OCUP==4 ~ 14,
go==2 & CAT_OCUP==NA ~ 14,
go==3 & CAT_OCUP==1 & tamano==2 ~ 3,
go==3 & CAT_OCUP==1 & tamano==1 ~ 4,
go==3 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 6,
go==3 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 6,
go==3 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 7,
go==3 & CAT_OCUP==3 & sector_act==2 ~ 8,
go==3 & CAT_OCUP==2 ~ 5,
go==3 & CAT_OCUP==4 ~ 5,
go==3 & CAT_OCUP==NA ~ 5,
go==4 & CAT_OCUP==1 & tamano==2 ~ 9,
go==4 & CAT_OCUP==1 & tamano==1 ~ 13,
go==4 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 10,
go==4 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 10,
go==4 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 11,
go==4 & CAT_OCUP==3 & sector_act==2 ~ 12,
go==4 & CAT_OCUP==2 ~ 14,
go==4 & CAT_OCUP==4 ~ 14,
go==4 & CAT_OCUP== NA ~ 14,
go==5 & CAT_OCUP==1 & tamano==2 ~ 9,
go==5 & CAT_OCUP==1 & tamano==1 ~ 13,
go==5 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 15,
go==5 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 15,
go==5 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 16,
go==5 & CAT_OCUP==3 & sector_act==2 ~ 17,
go==5 & CAT_OCUP==2 ~ 14,
go==5 & CAT_OCUP==4 ~ 14,
go==5 & CAT_OCUP== NA ~ 14,
go==6 & CAT_OCUP==1 & tamano==2 ~ 9,
go==6 & CAT_OCUP==1 & tamano==1 ~ 13,
go==6 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 19,
go==6 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 19,
go==6 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 20,
go==6 & CAT_OCUP==3 & sector_act==2 ~ 21,
go==6 & CAT_OCUP==2 ~ 18,
go==6 & CAT_OCUP==4 ~ 18,
go==6 & CAT_OCUP== NA ~ 18,
go==7 & CAT_OCUP==1 & tamano==2 ~ 25,
go==7 & CAT_OCUP==1 & tamano==1 ~ 25,
go==7 & CAT_OCUP==3 & sector_act==1 & tamano==2 ~ 22,
go==7 & CAT_OCUP==3 & sector_act==1 & is.na(tamano) ~ 22,
go==7 & CAT_OCUP==3 & sector_act==1 & tamano==1 ~ 23,
go==7 & CAT_OCUP==3 & sector_act==2 ~ 24,
go==7 & CAT_OCUP==4 ~ 25,
go==7 & CAT_OCUP==2 ~ 25,
go==7 & CAT_OCUP== NA ~ 25,
go==8 ~ 26,
go==9 ~ 27))Hasta aquí ya tenemos construido el CSO desagregado, que si bien permite una discriminación más precisa de la situación socio-ocupacional de las personas, sus 27 categorías dificultan la síntesis y el cruce con otras variables. En la Tabla 5.11, indicamos el código y la nomenclatura original que la autora asigna a cada posición en el texto (Torrado, 1998b, p. 226), el código que le asignamos nosotros para el uso en la sintaxis y la recodificación del CSO agregado que será revisado en la próxima sección.
Nº sintaxis |
Nº real |
CSO desagregado |
CSO agregado |
|---|---|---|---|
1 |
1.1 |
DIREC (ER - SPR. TE>5) |
1 |
2 |
1.2 |
DIREC (AS - SPR. TE>5) |
|
3 |
2.1.1 |
PROF (ER- SPR. >5) |
2 |
4 |
2.1.2 |
PROF (ER- SPR. <=5) |
|
5 |
2.2 |
PROF (CP) |
|
6 |
2.3.1 |
PROF (AS- SPR. >5) |
|
7 |
2.3.2 |
PROF (AS- SPR. <=5) |
|
8 |
2.4 |
PROF (AS- SPU) |
|
9 |
3 |
PPE |
3 |
10 |
4.1.1 |
TECN (AS -SPR. TE>5) |
4 |
11 |
4.1.2 |
TECN (AS -SPR. TE<=5) |
|
12 |
4.2 |
TECN (AS -SPU) |
|
13 |
5.1 |
PPA (ER - SPR. TE <=5) |
5 |
14 |
5.2 |
PPA (CP) |
|
15 |
6.1.1 |
EAV (AS - SPR. TE>5) |
6 |
16 |
6.1.2 |
EAV (AS - SPR. TE<=5) |
|
17 |
6.2 |
EAV (AS - SPU) |
|
18 |
7 |
TEA |
7 |
19 |
8.1.1 |
OCAL (AS - SPR. TE>5) |
8 |
20 |
8.1.2 |
OCAL (AS - SPR. TE<=5) |
|
21 |
8.2 |
OCAL (AS - SPU) |
|
22 |
9.1.1 |
ONCAL (AS - SPR. TE>5) |
9 |
23 |
9.1.2 |
ONCAL (AS - SPR. TE<=5) |
|
24 |
9.2 |
ONCAL (AS - SPU) |
|
25 |
10 |
TMARG |
10 |
26 |
11 |
EDOM |
11 |
27 |
12 |
Sin especificar CSO |
12 |
Fuente: elaboración propia en base a Torrado (1998) | |||
5.3.4 Creación del CSO agregado
Con el CSO desagregado construido, ya estamos en condiciones de colapsarlo y generar un CSO agregado, que permite una mejor aplicación para el análisis de la estructura social e indagar aspectos a un menor nivel de agregación del que se logra con una clasificación de clases sociales. En la Tabla 5.11 previo pudimos observar como los estratos son agregados hasta formar 12 grupos (uno de carácter residual, en este caso lo damos como valor perdido).
En el siguiente script elaboramos la variable cso_agg que guarda bajo formato numérico los grupos agregados del CSO y una variable de tipo factor (css_agg_factor) que nos permite trabajar con los grupos etiquetados. Finalmente, observaremos como se distribuye la población según el CSO agregado.
eph_ind_215 <- eph_ind_215 %>%
mutate(cso_agg = case_when(cso_desag <= 2 ~ 1, cso_desag >= 3 & cso_desag <=
8 ~ 2, cso_desag == 9 ~ 3, cso_desag >= 10 & cso_desag <= 12 ~ 4, cso_desag >=
13 & cso_desag <= 14 ~ 5, cso_desag >= 15 & cso_desag <= 17 ~ 6, cso_desag ==
18 ~ 7, cso_desag >= 19 & cso_desag <= 21 ~ 8, cso_desag >= 22 & cso_desag <=
24 ~ 9, cso_desag == 25 ~ 10, cso_desag == 26 ~ 11, cso_desag == 27 | is.na(cso_desag) ~
NA_real_))
eph_ind_215$cso_agg_factor <- factor(eph_ind_215$cso_agg, labels = c("DIREC", "PROF",
"PPE", "TECN", "PPA", "EAV", "TEA", "OCAL", "ONCAL", "TMARG", "EDOM"))
table(eph_ind_215$cso_agg_factor)
DIREC PROF PPE TECN PPA EAV TEA OCAL ONCAL TMARG EDOM
138 1325 226 3324 2482 4988 2273 6119 1841 272 1354 5.3.5 Creación esquema de clase
Por último ya estamos en condiciones de elaborar el sistema de clases que la autora propone (Torrado, 1998b, p. 235). Vamos a realizar dos versiones, una de 6 categorías (clase6) y otra de 3 (clase3). En cada caso, generaremos un variable factor, que nos permitirá el etiquetamiento y el mejor tratamiento de la variable.
eph_ind_215 <- eph_ind_215 %>%
mutate(clase6 = case_when(cso_agg == 1 ~ 1, (cso_agg == 2 & CAT_OCUP == 2) |
cso_agg == 3 | cso_agg == 5 ~ 2, (cso_agg == 2 & CAT_OCUP >= 3) | cso_agg ==
4 | cso_agg == 6 ~ 3, cso_agg == 7 ~ 4, cso_agg == 8 | cso_agg == 9 ~ 5,
cso_agg == 10 | cso_agg == 11 ~ 6))
eph_ind_215$clase6_factor <- factor(eph_ind_215$clase6, labels = c("Clase alta",
"Clase media autónoma", "Clase media asalariada", "Clase obrera autónoma",
"Clase obrera asalariada", "Clase obrera trabajadores marginales"))
eph_ind_215 <- eph_ind_215 %>%
mutate(clase3 = car::recode(eph_ind_215$clase6, "1=1; 2:3=2; 4:6=3"))
eph_ind_215$clase3_factor <- factor(eph_ind_215$clase3, labels = c("Clase alta",
"Clase media", "Clase obrera"))Para calcular la distribución de frecuencias ponderadas de la población por clase social, presentamos dos procedimientos. Uno, que es el que veníamos utilizando, a través de los comandos group_by y tally del paquete dplyr, y otro a través de la función freq del paquete summarytools. Este último nos devuelve una tabla similar al comando tabulate de STATA o del análisis de frecuencias que realiza SPSS. Asimismo, nos permite señalar que variable se utilizara para ponderar los resultados.
eph_ind_215 %>%
filter(!is.na(clase6_factor)) %>% #quitamos los casos perdidos del análisis
group_by(clase6_factor) %>%
tally(PONDERA) %>%
mutate(porcentaje = round((n/sum(n))*100, digits = 2))# A tibble: 6 × 3
clase6_factor n porcentaje
<fct> <dbl> <dbl>
1 Clase alta 49429 0.45
2 Clase media autónoma 1446840 13.1
3 Clase media asalariada 4095309 37.0
4 Clase obrera autónoma 1013705 9.15
5 Clase obrera asalariada 3708848 33.5
6 Clase obrera trabajadores marginales 758822 6.85
summarytools::freq(eph_ind_215$clase6_factor, weights = eph_ind_215$PONDERA, cumul = FALSE, report.nas = FALSE)Weighted Frequencies
eph_ind_215$clase6_factor
Type: Factor
Weights: PONDERA
Freq %
------------------------------------------ ------------- --------
Clase alta 49429.00 0.45
Clase media autónoma 1446840.00 13.07
Clase media asalariada 4095309.00 36.98
Clase obrera autónoma 1013705.00 9.15
Clase obrera asalariada 3708848.00 33.49
Clase obrera trabajadores marginales 758822.00 6.85
Total 11072953.00 100.00Como puede observarse, alcanzamos los mismos resultados, pero la función freq es más rápida y sencilla de aplicar para analizar distribuciones de frecuencias. Existen varios paquetes para R que permiten la elaboración de tablas y análisis de frecuencia, y summarytools es una de las posibilidades. Si están interesados, les sugerimos que busquen y encuentren aquel paquete y funciones que les resulte más cómodo para hacer sus análisis.
5.4 Operacionalización automática
Paquetes que utilizaremos en este subcapítulo:
En este apartado aprenderemos otra forma de operacionalizar esquemas de clasificación social a través de R. Para ello utilizaremos el paquete occupar, que permite, entre sus distintas funciones:
Convertir diferentes versiones de la CIUO 9 (68, 88, 08).
Creación de esquemas de clasificación (ISEI, SIOPS, EGP, ESeC) a partir de la CIUO.
Las ventajas de la utilización de este tipo de operacionalización es que podemos ahorrarnos una cantidad importante de tiempo, ya que no tendremos que invertirlo en escribir líneas y líneas de código. Al mismo tiempo, como veremos, nos permitirá la creación de al menos dos esquemas que son internacionalmente utilizados. Como desventaja, dependemos de la interpretación que los autores del paquete hicieron del proceso de operacionalización. Recordemos que operacionalizar implica decisiones teórico-metodológicas en la selección de variables y la combinación de categorías para la construcción de nuevas categorías (en este caso estratos y clases). Es decir, no podremos fácilmente modificar la propuesta de operacionalización ni adaptarla a nuestros objetivos e intereses.
Por ejemplo, el paquete no operacionaliza en forma correcta el esquema EGP, ya que asigna en forma errónea a los casos en algunas posiciones de clase. En el caso que se quiera utilizar dicho esquema, es recomendable recurrir a esquema ESeC, utilizado oficialmente en Europa, y que está basado en el EGP.
El paquete occupar esta basado en el proyecto implementado por Harry Ganzeboom de estandarización y armonización de medidas de posición de clase y estratificación 10. El mismo también se encuentra disponible para ser utilizado con SPSS. A continuación vamos a explorar como operacionalizar la escala ISEI utilizando dicho paquete.
Para instalar el paquete occupar es necesario tener instalado el paquete devtools. A continuación dejamos los pasos de instalación:
install.packages("devtools")
devtools::install_github("DiogoFerrari/occupar", dependencies = F)5.4.1 Operacionalizando la escala ISEI
Recordemos que la escala ISEI no es un esquema discreto de clases sociales, sino que esta basado en un enfoque gradacional, en donde a cada ocupación se le otorga un puntaje, estandarizado internacionalmente, considerando como factores a la edad, la educación y la ocupación.
Utilizaremos la misma base que venimos explorando: la EPH del segundo trimestre de 2015 con el agregado de la ocupación codificada en la CIUO-08. La función es relativamente sencilla, se llama isco08toISEI08 y sólo debemos señalarle donde se encuentra la variable CIUO. A continuación solicitaremos un resumen de las principales medidas de tendencia central y de posición.
eph_ind_215$isei <- isco08toISEI08(eph_ind_215$PP04D_CIUO)
summary(eph_ind_215$isei) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
12 23 31 38 49 89 35722
eph_ind_215 %>%
select(PP04D_CIUO, isei) %>% #selecciono las variables de ocupación
filter(!is.na(isei)) %>% #filtro los casos con valores perdidos
head(n = 10)# A tibble: 10 × 2
PP04D_CIUO isei
<fct> <dbl>
1 7233 31.7
2 9112 14.2
3 7411 36.4
4 8331 26.8
5 7231 30.8
6 2262 81.1
7 9214 11.7
8 5322 21.6
9 7522 25.2
10 5223 28.5La ocupación peor posicionada es la que presenta un valor de 11,56, mientras que la mejor posicionada 88,96. La ocupación que divide a la muestra en dos (mediana) tiene un valor de 30,78 y el promedio es 35,78.
Por otro lado, pedimos también que nos muestren algunas correspondencias entre los valores de la codificación en CIUO y los puntajes del ISEI. Claramente los valores más bajos del ISEI, se corresponden con valores más bajos de la CIUO:
eph_ind_215 %>%
ggplot(aes(x = isei, weight = PONDERA)) + geom_histogram(bins = 20) + labs(y = "Frecuencia",
caption = "Elaboración propia en base a EPH-INDEC 2015") + theme(plot.caption = element_text(size = 9),
axis.title.x = element_blank(), axis.title.y = element_text(size = 10), axis.text.x = element_text(size = 10),
axis.text.y = element_text(size = 10)) + scale_x_continuous(breaks = seq(10,
90, 5)) + scale_y_continuous(labels = scales::comma, breaks = seq(0, 1500000,
100000))Gráfico 5.2: Histograma de frecuencias la escala ISEI
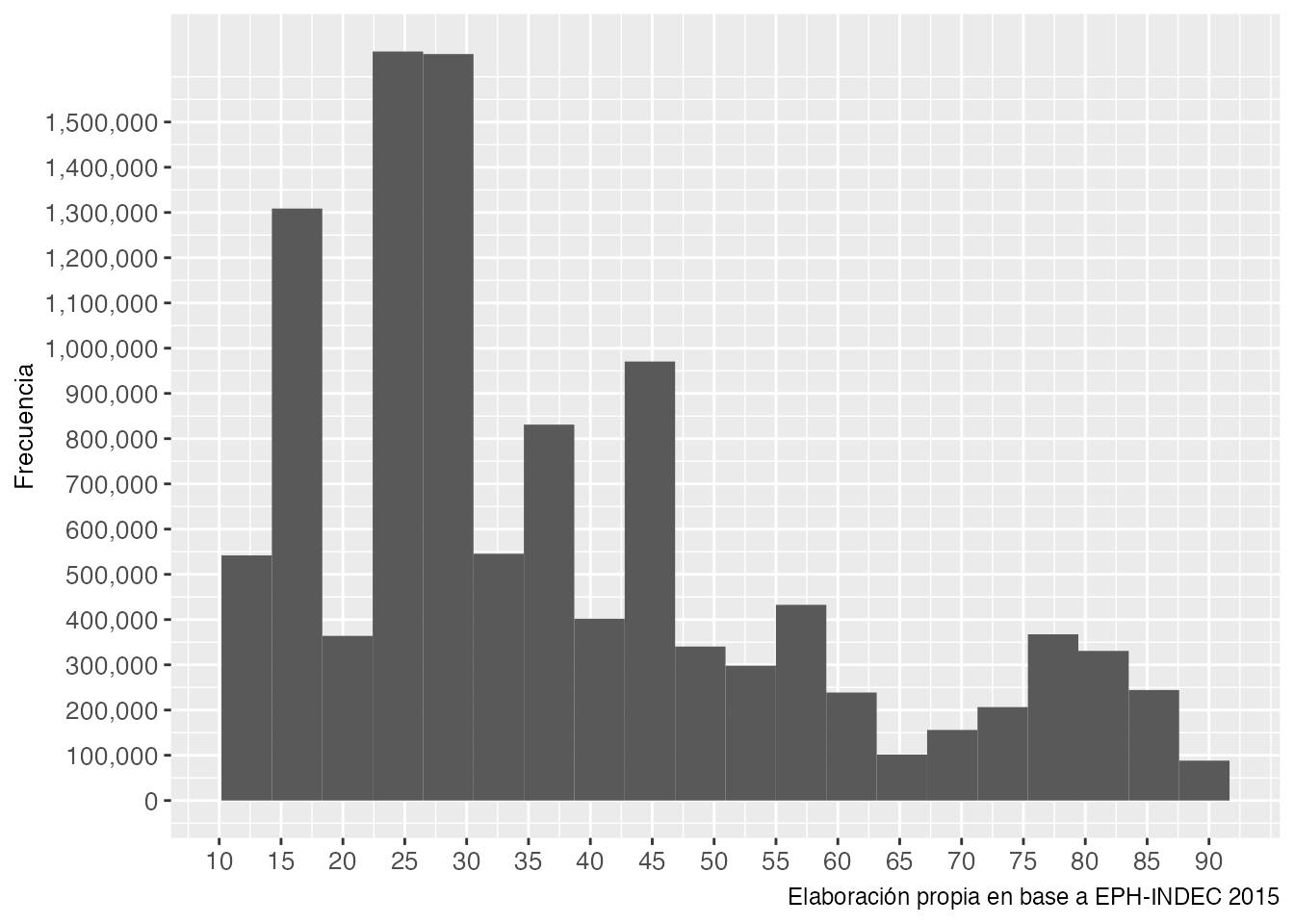
El histograma nos muestra donde se concentran las personas según sus ocupaciones. De esta forma, la mayor parte de la población se encuentra entre el puntaje 15 y 43 de la escala. Por el contrario, las ocupaciones mejores puntadas tienen una menor proporción de personas.
5.5 Unidades de análisis y clases sociales
5.5.1 Breve discusión teórica11
Una vez construido empíricamente nuestro esquema de clases, es importante definir el universo de análisis a considerar, desde el punto de vista de la pertenencia de clase. Si bien está decisión es importante realizarla en etapas previas de la investigación, nos referimos a la importancia en la resolución metodológica de dicha cuestión. Hay varias formas de proceder, pero digamos que en primer lugar, es necesario establecer si nuestra población objetivo serán individuos u hogares. En el primer caso, como señala Torrado (1998b, pp. 236–237), sería necesario considerar a la PEA, mientras que en el segundo caso a algún indicador del hogar como puede ser la posición del jefe/a activo/a de los hogares particulares.
La primera de estas opciones tiene la ventaja que permite una imagen más fiel de las características del sistema productivo al cual se está haciendo referencia, aunque sólo abarca a una población pequeña de la población. La consideración de los hogares, implica en este sentido, un aumento en la población analizada (por ejemplo, todos los hogares con jefe/a activo/a), a la vez que permite una mejor captación del conocimiento de la estructura social respecto a la medición de las condiciones de vida y comportamientos diversos, que únicamente pueden ser atribuidos a la esfera del hogar (Torrado, 1998b, p. 238). En este sentido, cada unidad de análisis nos permiten observar fenómenos distintos de la realidad social y es decisión de los investigadores que camino seguir en función de los objetivos propuestos.
Un segundo aspecto a considerar es, parafraseando a Crompton (2008, p. 124), “el problema de las mujeres”. Tanto al considerar como unidad de análisis a los individuos o a los hogares, los estudios de clases y movilidad social, han estado largamente dominados por enfoques que asignaban a las mujeres la misma posición que la del jefe de familia. Más allá de la larga discusión que abarcó gran parte de los años 80 y que mantiene sus repercusiones en la actualidad (Gómez Rojas, 2011; Riveiro, 2017), resulta totalmente sesgado tanto teórico como metodológicamente la subsunción de las situaciones de las mujeres a la de los varones.
En este sentido, en forma resumida, cuatro enfoques se encuentran fundamentalmente en la bibliografía del análisis de clase para solucionar esta problemática (Feito Alonso, 1995b). En primer lugar, puede citarse el enfoque tradicional, defendido en un primer momento por Goldthorpe (1983), que sostiene que los hogares deben ser considerados como unidad de análisis, aunque debe ser la posición del varón jefe de familia quien le otorgue al grupo su posición de clase. En un segundo lugar podemos señalar el enfoque de dominancia, propuesto por Erikson (1984), que se basa en la determinación de la posición de clase del hogar a partir de la situación de clase del cónyuge cuya inserción sea más decisiva de cara a la determinación de intereses, patrones de consumo, condiciones de vivienda, etc. En términos simplificados, dicho enfoque, deriva la condición de clase del hogar de la posición mejor situada entre los cónyuges. Un tercer enfoque considera conjuntamente a la posición de ambos cónyuges para caracterizar al hogar. De lo que se trata es de generar una tipología de hogares que clasifique a los mismos en función de su carácter homogéneo (ambos cónyuges pertenecen a la misma clase) y heterogéneo (ambos cónyuges pertenecen a clases distintas). Dicho enfoque es subsidiario, principalmente, de la propuesta de Wright (1992) al considerar las posiciones contradictorias (mediatas e inmediatas) dentro de la estructura de clases. Finalmente, un cuarto enfoque plantea la necesidad de considerar las posiciones de los varones y mujeres de forma individual, a partir de su propia situación de clase y sin tomar al hogar como unidad de análisis.
5.5.2 Opciones metodológicas
En esta sección vamos a explorar tres formas de abordar la estructura de clases a partir de la selección de distintas unidades de análisis: considerando a la población ocupada, considerando al hogar a través de la jefatura y considerando al hogar a través de la dominancia. Como señalamos, esta selección no es exhaustiva ni superadora. La elección de cada uno de los abordajes dependera de decisiones teórico-metodológicas.
En el primer caso, para considerar al universo de estudio de la población ocupada sólo necesitaremos filtrar nuestra base únicamente seleccionando a aquellos individuos que para la variable ESTADO se encuentran en condición de ocupados (1).
base_PO <- eph_ind_215 %>%
filter(ESTADO == 1) # Creamos una nueva base con el filtro de la población ocupada
summarytools::freq(base_PO$clase6_factor, weights = base_PO$PONDERA, justify = "center",
cumul = FALSE)Weighted Frequencies
base_PO$clase6_factor
Type: Factor
Weights: PONDERA
Freq % Valid % Total
------------------------------------------ ------------- --------- ---------
Clase alta 49429.00 0.45 0.44
Clase media autónoma 1446840.00 13.07 12.99
Clase media asalariada 4095309.00 36.98 36.77
Clase obrera autónoma 1013705.00 9.15 9.10
Clase obrera asalariada 3708848.00 33.49 33.30
Clase obrera trabajadores marginales 758822.00 6.85 6.81
<NA> 63766.00 0.57
Total 11136719.00 100.00 100.00 De esta forma, observamos que la población ocupada asciende a 11.136.719, considerando 63.766 valores perdidos, es decir, personas que no pudieron ser clasificadas bajo esquema empleado. Esta tabla nos brindaría una imagen de cómo que conforma la estructura de clases en la población ocupada.
Si en cambio lo que queremos observar es al universo de los hogares, utilizaremos las características económicas-laborales de uno de los miembros del hogar para caracterizar a toda la unidad. En el primer caso, nos basaremos en la jefatura del hogar. Para ello, filtraremos aquellos casos que sean jefe/a (1) en la variable CH03.
base_jefatura <- eph_ind_215 %>%
filter(CH03 == 1) # Nos quedamos únicamente con los/las jefe/as de hogar
summarytools::freq(base_jefatura$clase6_factor, weights = base_jefatura$PONDERA,
justify = "center", cumul = FALSE)Weighted Frequencies
base_jefatura$clase6_factor
Type: Factor
Weights: PONDERA
Freq % Valid % Total
------------------------------------------ ------------ --------- ---------
Clase alta 28725.00 0.51 0.34
Clase media autónoma 792515.00 14.09 9.42
Clase media asalariada 1922384.00 34.19 22.84
Clase obrera autónoma 618087.00 10.99 7.34
Clase obrera asalariada 1941096.00 34.52 23.06
Clase obrera trabajadores marginales 320537.00 5.70 3.81
<NA> 2792656.00 33.18
Total 8416000.00 100.00 100.00 Si comparamos con la tabla anterior, los valores han cambiado. Esto se debe a que pasamos de considerar individuos a considerar hogares. El número total de hogares es de 8.416.000 y los casos perdidos ascienden a 2.792.656, grupo conformado por hogares con jefatura desocupada o inactiva.
Finalmente podemos considerar el enfoque de dominancia. Este es algo más complejo en su elaboración, ya que es necesario aplicar una serie de pasos. De este modo, definimos a la posición de clase social del hogar como aquella ocupada por el cónyuge que posee la posición más aventajada. En los casos de hogares no nucleares o con el núcleo incompleto (ausencia de uno de los cónyuges), se tomará directamente la clase del jefe/a.
# 1) Selecciono solo a jefe/as y cónyuges
base_dominancia <- eph_ind_215 %>%
filter(CH03 == 1 | CH03 == 2)
# 2) Agrupando por vivienda (CODUSU) y hogar (NRO_HOGAR), creo una nueva variable que compute cual es la posición de clase más alta, que este caso es el valor más bajo (min), ya que las clases se ordenan de menor a mayor en las variables.
base_dominancia <- base_dominancia %>%
group_by(CODUSU, NRO_HOGAR) %>%
mutate(clase_dom = min(clase6, na.rm = TRUE))
# 3) Identifico qué cónyuge es el dominante.
base_dominancia <- base_dominancia %>%
mutate(dom = case_when(clase6 == clase_dom ~ 1, # dominante
clase6 > clase_dom ~ 0)) # no dominante
# 4) Identifico a los hogares en el que los cónyuges comparten la dominancia, es decir, tienen la misma clase. Para eso sumo (dom_sum) dentro del hogar la variable "dom". Luego a partir de ese resultado puedo definir quien es el miembro dominante y otorgar la dominancia al jefe/a en el caso que ambos tengan la misma clase.
base_dominancia <- base_dominancia %>%
group_by(CODUSU, NRO_HOGAR) %>%
mutate(dom_sum = sum(dom, na.rm = TRUE))
base_dominancia <- base_dominancia %>%
mutate(dominancia = case_when(dom == 1 & dom_sum == 1 ~ 1, #dominante
dom == 0 & dom_sum == 1 ~ 0, # no dominante
dom == 1 & dom_sum == 2 & CH03 == 1 ~ 1, # dominante por ser jefe de hogar
dom == 1 & dom_sum == 2 & CH03 == 2 ~ 0)) # no dominante por no ser jefe de hogar
# 5) Filtro la base con los "dominantes" y borro las variables intermedias que cree.
base_dominancia <- base_dominancia %>%
filter(dominancia == 1)
base_dominancia$dom <- NULL
base_dominancia$dom_sum <- NULL
summarytools::freq(base_dominancia$clase6_factor, weights = base_dominancia$PONDERA, justify = "center", cumul = FALSE)Weighted Frequencies
base_dominancia$clase6_factor
Type: Factor
Weights: PONDERA
Freq % Valid % Total
------------------------------------------ ------------ --------- ---------
Clase alta 45732.00 0.75 0.75
Clase media autónoma 1027302.00 16.95 16.95
Clase media asalariada 2229496.00 36.80 36.80
Clase obrera autónoma 621547.00 10.26 10.26
Clase obrera asalariada 1831160.00 30.22 30.22
Clase obrera trabajadores marginales 303996.00 5.02 5.02
<NA> 0.00 0.00
Total 6059233.00 100.00 100.00 En este caso, luego de aplicar las transformaciones, contamos con 6.059.233 hogares clasificados a partir de la posición dominante de uno de lo cónyuges.